Entrega até 22/11/2016
1) Determine o valor de x.

2) Uma ponte deve ser construída sobre um rio, unindo os pontos A e B, como ilustrado na figura a seguir. Para calcular o comprimento AB, escolhe-se um ponto C, na mesma margem que está o ponto B, e medem-se os ângulos CBA = 57º e ACB = 59º. Sabendo-se que BC mede 30 m., calcule, em metros, a distância AB (Dado: use as aproximações sen 59° ≈ 0,87 e sen 64º ≈ 0,90)

3) No triângulo abaixo, determine as medidas de x e y.

4) Num triângulo ABC, o lado BC = 8√ 2 cm, Â = 30º e Ĉ = 45o , calcule a medida do lado AB.
5) Dois lados de um triângulo medem 6cm e 10cm, e formam entre si um ângulo de 60º. Determine a medida do terceiro lado desse triângulo.
6) Considere um triangulo em que um dos ângulos mede 75° e o lado oposto a ele mede 90cm. Outro ângulo mede 80°. Calcule a medida do lado oposto ao ângulo de 80°. Dado: sen75=0,966; sen80=0,985.
10)Em um triângulo, os lados de medidas 6√3 cm e 8 cm formam um ângulo de 30º. Determine a medida do terceiro lado.

3) No triângulo abaixo, determine as medidas de x e y.

4) Num triângulo ABC, o lado BC = 8√ 2 cm, Â = 30º e Ĉ = 45o , calcule a medida do lado AB.
5) Dois lados de um triângulo medem 6cm e 10cm, e formam entre si um ângulo de 60º. Determine a medida do terceiro lado desse triângulo.
6) Considere um triangulo em que um dos ângulos mede 75° e o lado oposto a ele mede 90cm. Outro ângulo mede 80°. Calcule a medida do lado oposto ao ângulo de 80°. Dado: sen75=0,966; sen80=0,985.
7) Dois lados de um triângulo medem 6m e 10m e formam entre si um
ângulo de 120º. Determinar a medida do terceiro lado. Cos 120º= -1/2
8) Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine o valor do cos Â.
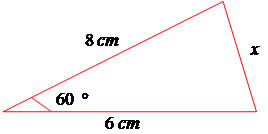
9) Determine o valor do lado oposto ao ângulo de 60º. Observe figura a seguir:
.jpg)
9) Determine o valor do lado oposto ao ângulo de 60º. Observe figura a seguir:
.jpg)
10)Em um triângulo, os lados de medidas 6√3 cm e 8 cm formam um ângulo de 30º. Determine a medida do terceiro lado.